1. 简介
NLP的底层任务由易到难大致可以分为词法分析、句法分析和语义分析。分词是词法分析(还包括词性标注和命名实体识别)中最基本的任务,可以说既简单又复杂。说简单是因为分词的算法研究已经很成熟了,大部分的准确率都可以达到95%以上,说复杂是因为剩下的5%很难有突破,主要因为三点:
- 粒度,不同应用对粒度的要求不一样,比如“苹果手机”可以是一个词也可以是两个词
- 歧义,比如“下雨天留人天留我不留”
- 未登录词,比如“skrrr”、“打call”等新兴词语
然而,在真实的应用中往往会因为以上的难点造成分词效果欠佳,进而影响之后的任务。对于追求算法表现的童鞋来说,不仅要会调分词包,也要对这些基础技术有一定的了解,在做真正的工业级应用时有能力对分词器进行调整。这篇文章不是着重介绍某个SOTA成果,而是对常用的分词算法(不仅是机器学习或神经网络,还包括动态规划等)以及其核心思想进行介绍。
2. 分词算法
我认为分词算法根据其核心思想主要分为两种,第一种是基于字典的分词,先把句子按照字典切分成词,再寻找词的最佳组合方式;第二种是基于字的分词,即由字构词,先把句子分成一个个字,再将字组合成词,寻找最优的切分策略,同时也可以转化成序列标注问题。归根结底,上述两种方法都可以归结为在图或者概率图上寻找最短路径的问题。接下来将以“他说的确实在理”这句话为例,讲解各个不同的分词算法核心思想。
2.1 基于词典的分词
2.1.1 最大匹配分词算法
最大匹配分词寻找最优组合的方式是将匹配到的最长词组合在一起。主要的思路是先将词典构造成一棵Trie树,也称为字典树,如下图:
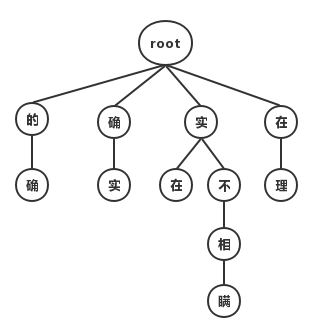
Trie树由词的公共前缀构成节点,降低了存储空间的同时提升查找效率。最大匹配分词将句子与Trie树进行匹配,在匹配到根结点时由下一个字重新开始进行查找。比如正向(从左至右)匹配“他说的确实在理”,得出的结果为“他/说/的确/实在/理”。如果进行反向最大匹配,则为“他/说/的/确实/在理”。
可见,词典分词虽然可以在O(n)时间对句子进行分词,但是效果很差,在实际情况中基本不使用此种方法。
2.1.2 最短路径分词算法
最短路径分词算法首先将一句话中的所有词匹配出来,构成词图(有向无环图DAG),之后寻找从起始点到终点的最短路径作为最佳组合方式,引用《统计自然语言处理》中的图:
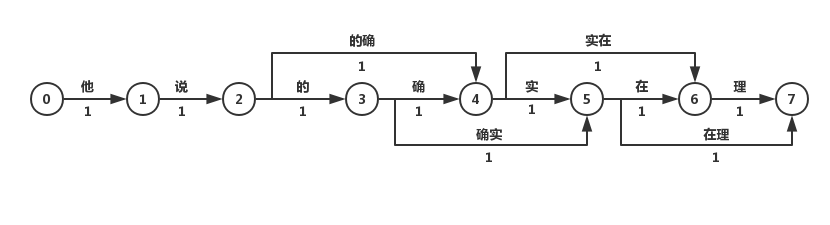
我们认为图中每个词的权重都是相等的,因此每条边的权重都为1。
在求解DAG图的最短路径问题时,总是要利用到一种性质:即两点之间的最短路径也包含了路径上其他顶点间的最短路径。比如S->A->B->E为S到E到最短路径,那S->A->B一定是S到B到最短路径,否则会存在一点C使得d(S->C->B)<d(S->A->B),那S到E的最短路径也会变为S->C->B->E,这就与假设矛盾了。利用上述的最优子结构性质,可以利用贪心算法或动态规划两种求解算法:
1. 最短路径分词算法
基于Dijkstra算法求解最短路径。该算法适用于所有带权有向图,求解源节点到其他所有节点的最短路径,并可以求得全局最优解。Dijkstra本质为贪心算法,在每一步走到当前路径最短的节点,递推地更新原节点到其他节点的距离。针对当前问题,Dijkstra算法的计算结果为:“他/说/的/确实/在理“。可见最短路径分词算法可以满足部分分词要求。但当存在多条距离相同的最短路径时,Dijkstra只保存一条,对其他路径不公平,也缺乏理论依据。
2. N-最短路径分词算法
N-最短路径分词是对Dijkstra算法的扩展,在每一步保存最短的N条路径,并记录这些路径上当前节点的前驱,在最后求得最优解时回溯得到最短路径。该方法的准确率优于Dijkstra算法,但在时间和空间复杂度上都更大。
2.1.3 基于n-gram model的分词算法
在前文的词图中,边的权重都为1。而现实中却不一样,常用词的出现频率/概率肯定比罕见词要大。因此可以将求解词图最短路径的问题转化为求解最大概率路径的问题,即分词结果为“最有可能的词的组合“。计算词出现的概率,仅有词典是不够的,还需要有充足的语料。因此分词任务已经从单纯的“算法”上升到了“建模”,即利用统计学方法结合大数据挖掘,对“语言”进行建模。
语言模型的目的是构建一句话出现的概率p(s),根据条件概率公式我们知道:
而要真正计算“他说的确实在理”出现的概率,就必须计算出上述所有形如 n=1,...,6%20的概率,计算量太过庞大,因此我们近似地认为:
其中 , 为字或单词。我们将上述模型成为二元语言模型(2-gram%20model)。类似的,如果只对词频进行统计,则为一元语言模型。由于计算量的限制,在实际应用中n一般取3。
我们将基于词的语言模型所统计出的概率分布应用到词图中,可以得到词的概率图:
对该词图用2.1.2中的算法求解最大概率的路径,即可得到分词结果。
2.2 基于字的分词
与基于词典的分词不同的是,基于字的分词事先不对句子进行词的匹配,而是将分词看成序列标注问题,把一个字标记成B(Begin), I(Inside), O(Outside), E(End), S(Single)。因此也可以看成是每个字的分类问题,输入为每个字及其前后字所构成的特征,输出为分类标记。对于分类问题,可以用统计机器学习或神经网络的方法求解。
统计机器学习方法通过一系列算法对问题进行抽象,进而得到模型,再用得到的模型去解决相似的问题。也可以将模型看成一个函数,输入X,得到f(X)=Y。另外,机器学习中一般将模型分为两类:生成式模型和判别式模型,两者的本质区别在于X和Y的生成关系。生成式模型以“输出Y按照一定的规律生成输入X”为假设对P(X,Y)联合概率进行建模;判别式模型认为Y由X决定,直接对后验概率P(Y|X)进行建模。两者各有利弊,生成模型对变量的关系描述更加清晰,而判别式模型容易建立和学习。下面对几种序列标注方法做简要介绍。
2.2.1 生成式模型分词算法
生成式模型主要有n-gram模型、HMM隐马尔可夫模型、朴素贝叶斯分类等。在分词中应用比较多的是n-gram模型和HMM模型。如果将2.1.3中的节点由词改成字,则可基于字的n-gram模型进行分词,不过这种方法的效果没有基于词的效果要好。
HMM模型认为在解决序列标注问题时存在两种序列,一种是观测序列,即人们显性观察到的句子,而序列标签是隐状态序列,即观测序列为X,隐状态序列是Y,因果关系为Y->X。因此要得到标注结果Y,必须对X的概率、Y的概率、P(X|Y)进行计算,即建立P(X,Y)的概率分布模型。例句的隐马尔科夫序列如下图:
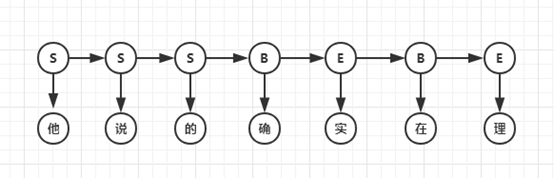
HMM模型是常用的分词模型,基于Python的jieba分词器和基于Java的HanLP分词器都使用了HMM。要注意的是,该模型创建的概率图与上文中的DAG图并不同,因为节点具有观测概率,所以不能再用上文中的算法求解,而应该使用Viterbi算法求解最大概率的路径。
2.2.2 判别式模型分词算法
判别式模型主要有感知机、SVM支持向量机、CRF条件随机场、最大熵模型等。在分词中常用的有感知机模型和CRF模型:
1. 平均感知机分词算法
感知机是一种简单的二分类线性模型,通过构造超平面,将特征空间(输入空间)中的样本分为正负两类。通过组合,感知机也可以处理多分类问题。但由于每次迭代都会更新模型的所有权重,被误分类的样本会造成很大影响,因此采用平均的方法,在处理完一部分样本后对更新的权重进行平均。
2. CRF分词算法
CRF可以看作一个无向图模型,对于给定的标注序列Y和观测序列X,对条件概率P(Y|X)进行定义,而不是对联合概率建模。CRF可以说是目前最常用的分词、词性标注和实体识别算法,它对未登陆词有很好的识别能力,但开销较大。
2.2.3 神经网络分词算法
在NLP中,最常用的神经网络为循环神经网络(RNN,Recurrent Neural Network),它在处理变长输入和序列输入问题中有着巨大的优势。LSTM为RNN变种的一种,在一定程度上解决了RNN在训练过程中梯度消失和梯度爆炸的问题。双向(Bidirectional)循环神经网络分别从句子的开头和结尾开始对输入进行处理,将上下文信息进行编码,提升预测效果。
目前对于序列标注任务,公认效果最好的模型是BiLSTM+CRF。结构如图:
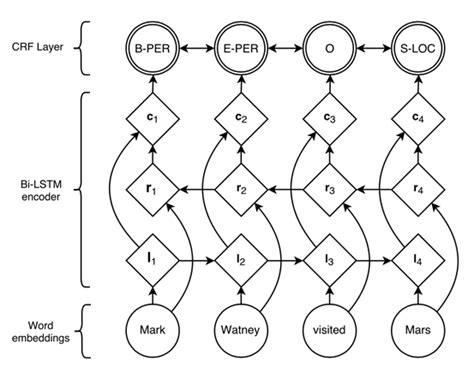
利用双向循环神经网络BiLSTM,相比于上述其它模型,可以更好的编码当前字等上下文信息,并在最终增加CRF层,核心是用Viterbi算法进行解码,以得到全局最优解,避免B,S,E这种标记结果的出现。
3. 分词算法中的数据结构
前文主要讲了分词任务中所用到的算法和模型,但在实际的工业级应用中,仅仅有算法是不够的,还需要高效的数据结构进行辅助。
3.1 词典
中文有7000多个常用字,56000多个常用词,要将这些数据加载到内存虽然容易,但进行高并发毫秒级运算是困难的,这就需要设计巧妙的数据结构和存储方式。前文提到的Trie树只可以在O(n)时间完成单模式匹配,识别出“的确”后到达Trie树对也节点,句子指针接着指向“实”,再识别“实在”,而无法识别“确实”这个词。如果要在O(n)时间完成多模式匹配,构建词图,就需要用到Aho-Corasick算法将模式串预处理为有限状态自动机,如模式串是he/she/his/hers,文本为“ushers”。构建的自动机如图:
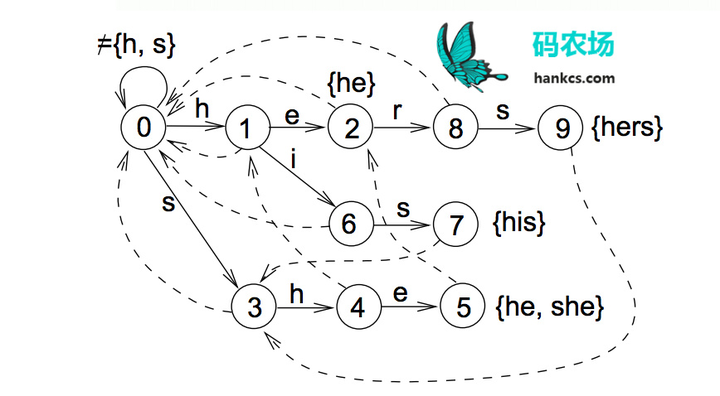
这样,在第一次到叶节点5时,下一步的匹配可以直接从节点2开始,一次遍历就可以识别出所有的模式串。
对于数据结构的存储,一般可以用链表或者数组,两者在查找、插入和删除操作的复杂度上各有千秋。在基于Java的高性能分词器HanLP中,作者使用双数组完成了Trie树和自动机的存储。
3.2 词图
图作为一种常见的数据结构,其存储方式一般有两种:
1. 邻接矩阵
邻接矩阵用数组下标代表节点,值代表边的权重,即d[i][j]=v代表节点i和节点j间的边权重为v。如下图:
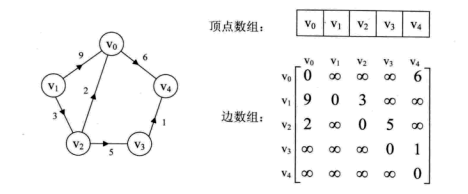
用矩阵存储图的空间复杂度较高,在存储稀疏图时不建议使用。
2. 邻接表
邻接表对图中的每个节点建立一个单链表,对于稀疏图可以极大地节省存储空间。第i个单链表中的节点表示依附于顶点i的边,如下图:
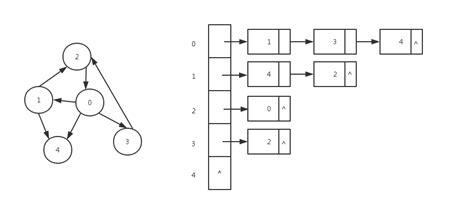
在实际应用中,尤其是用Viterbi算法求解最优路径时,由于是按照广度优先的策略对图进行遍历,最好是使用邻接表对图进行存储,便于访问某个节点下的所有节点。
4. 总结
分词作为NLP底层任务之一,既简单又重要,很多时候上层算法的错误都是由分词结果导致的。因此,对于底层实现的算法工程师,不仅需要深入理解分词算法,更需要懂得如何高效地实现。而对于上层应用的算法工程师,在实际分词时,需要根据业务场景有选择地应用上述算法,比如在搜索引擎对大规模网页进行内容解析时,对分词对速度要求大于精度,而在智能问答中由于句子较短,对分词的精度要求大于速度。